Des dés aux données : de l'importance des nombres aléatoires (partie 2/2)

Dans notre premier article, nous avons déterminé le rôle crucial de la génération de nombres aléatoires dans de nombreux domaines techniques ainsi que de la nécessité de tester cette génération.

Dans cet article, nous présenterons les concepts statistiques permettant d’analyser les générateurs de nombres aléatoires.

Dans un second temps, nous présenterons un nouvel outil permettant de tester statistiquement les générateurs de nombres aléatoires :  Random Test Tool (RTT) [https://github.com/xmco/random_test_tool/].

Enfin, nous synthétiserons de bonnes pratiques d’implémentation pour l’utilisation de nombres aléatoires et une méthodologie d’audit de système de la génération de nombres aléatoires sera proposée.

Statistiques et générateurs aléatoires

Entropie de Shannon et distributions uniformes

Les termes “entropie” et “aléatoire” sont parfois confondus. Pourtant, ces deux concepts sont bien liés et il est nécessaire de bien les comprendre pour pouvoir présenter le fonctionnement de générateurs aléatoires ainsi que la manière de les tester.

Définition : L’entropie au sens de Shannon est la mesure de la quantité d’information contenue dans un message.

Mathématiquement, elle se calcule de la manière suivante :

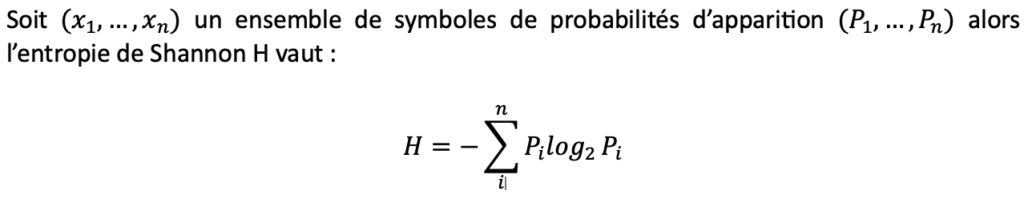
Définition : Un message est un ensemble de signes visant à transmettre une information. Il implique un codage par l’émetteur et un décodage par le récepteur.

Définition : Une information désigne, parmi un ensemble d’évènements, un ou plusieurs évènements possibles [INFOR].

Définition : Une distribution uniforme (discrète) est une distribution où la variable aléatoire a une chance équiprobable de réaliser chaque modalité. Par exemple pour un lancer de dé à 6 faces, chaque face a 1 chance sur 6 d’apparaître.

Par exemple, pour estimer “l’entropie de la langue française”, on pourrait se servir des fréquences d’apparition de chaque lettre dans un texte en français puis se servir de la formule définie ci-dessus.

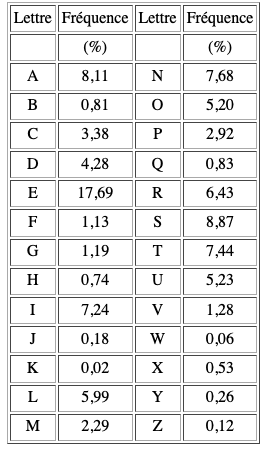
On obtient une valeur H_fr ≈ 9,95. Cela signifie selon la théorie de l’information que le nombre minimal de bits pour encoder un message en français est de 4.

Selon cette définition, l’entropie de Shannon est maximale quand la répartition des symboles suit une distribution uniforme [ENTRO_MATH].

L’aléatoire quant à lui est intrinsèquement lié à la notion d’imprédictibilité. En effet, pour une suite de symboles produite de manière aléatoire, on veut que la probabilité de succès pour prédire le prochain symbole soit 1/N si N est le nombre de symboles possibles. Cela signifie donc que pour qu’une séquence soit aléatoire (au sens cryptographique), il faut que les symboles soient produits selon une distribution uniforme.

Ainsi, comme vu précédemment, une séquence produite aléatoirement maximise également l’entropie de Shannon.

Tests statistiques et p-values

Définitions

La caractéristique fondamentale recherchée chez un générateur aléatoire est la capacité à générer des séquences qui soient imprédictibles.

Pour vérifier cette propriété sur un générateur aléatoire, les nombres générés sont soumis à une batterie de tests statistiques.

Définition : Un test statistique cherche à vérifier une hypothèse. Dans le cas de la validation d’un générateur aléatoire, l’hypothèse serait « ce générateur génère des séquences aléatoires ».

Définition : H0/H1 : En mathématiques, l’hypothèse que l’on souhaite vérifier s’appelle l’hypothèse nulle H0 et la réciproque (ici le générateur ne génère pas de séquences aléatoires) s’appelle l’hypothèse alternative H1 [STATS].

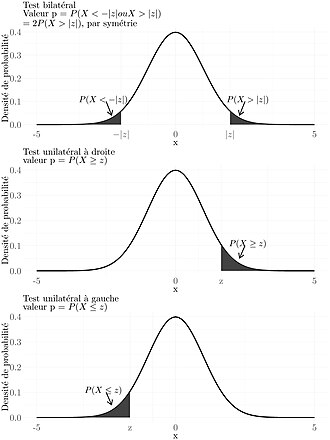
Définition : P-value : Un test statistique permet de calculer une valeur appelée la “valeur-p” ou “p-value” qui représente la probabilité d’obtenir des données aussi extrêmes que celles observées dans le cas où l’hypothèse nulle est correcte.

Ainsi, une p-value proche de 0 signifie que si l’hypothèse H0 était vraie, la probabilité d’obtenir une suite de nombres aussi rare serait également proche de 0.

Définition : Seuil : Généralement, quand on établit un test statistique, on définit également un seuil auquel on va comparer la p-value obtenue pour déterminer si le test et réussit ou non.
Ce seuil est généralement compris entre 0.05 et 0.001 selon la signifiance que l’on veut donner au test.

Si la p-value obtenue est supérieure au seuil, on accepte l’hypothèse H0 : le test est réussi.

Détecter l’aléatoire : quels tests choisir ?

En pratique, pour valider un générateur aléatoire, on veut vérifier qu’un attaquant soit incapable de prédire les nombres futurs avec la connaissance des nombres passés.

Ainsi l’objectif des tests statistiques sera des détecter les propriétés suivantes :

• Équiprobabilité des nombres générés
• Absence de périodicité
• Absence de motifs récurrents
• Absence de corrélation entre les nombres générés

Différents types de générateurs de nombres aléatoires.

Il existe différents types de générateurs aléatoires dont l’usage dépend des contraintes en termes de qualité d’aléatoire, de performance et de facilité de génération.

Les plus communs sont les PRNG (Pseudo Random Number Generator), basés sur des fonctions mathématiques. Ces générateurs ont un état interne depuis lequel est dérivé un nombre donné en sortie. Une opération est effectuée entre chaque appel du PRNG afin de modifier son état interne de manière chaotique.

Afin de définir un état interne initial, un PRNG est initialisé avec une graine (“seed”), d’une longueur dépendant de la taille de la mémoire de l’algorithme choisi.

Pour chaque nouvelle initialisation d’un PRNG avec une même seed, la suite de nombre fournis par le générateur sera identique.

Un exemple de PRNG est le Générateur de Congruence Linéaire, ou “LCG”. Ce dernier fonctionne à partir d’une équation de la forme suivante :

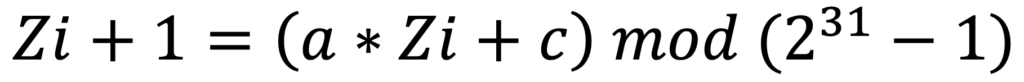
Les CSPRNG (Crypto-Safe Pseudo Random Number Generator) sont une catégorie de PRNG ayant des caractéristiques leur permettant d’être utilisés à des fins cryptographiques (génération de secrets / clés) :

• Chaque nombre fourni par le CSPRNG doit avoir une probabilité égale d’être tiré.
• Il est impossible d’identifier l’état interne du CSPRNG à partir des nombres générés.
• Il est impossible de trouver les nombres ayant été générés avant, ou bien qui seront générés après une quelconque suite de nombres donnée.
• Si l’état interne du CSPRNG est révélé, il doit être impossible de retrouver les nombres ayant été générés précédemment.
• L’état interne du CSPRNG doit être assez large pour qu’un attaquant ne puisse jamais énumérer tous les états possibles.

La plupart des PRNG ne respectent pas ces critères. Il est nécessaire d’utiliser un CSPRNG pour toute utilisation ayant trait à la sécurité ou à la cryptographie.

Ces caractéristiques ne rendent pas l’utilisation d’un CSPRNG infaillible. En effet, ces générateurs sont également initialisés à partir d’une seed. Si cette seed est prédictible (utilisation du timestamp, d’une adresse mémoire, d’un nom d’utilisateur, ou d’une longueur inférieure ou égale à 32 bits…), alors un attaquant pourrait tout de même énumérer l’ensemble des suites de nombres pouvant être générées par le CSPRNG (cf. notre précédent article sur l’aléatoire).

Par exemple, dans les systèmes d’exploitation basés sur Unix, un CSPRNG est disponible sous la forme des fichiers /dev/random et /dev/urandom. La seed utilisée est générée par différentes sources physiques relatives au fonctionnement du système comme l’état des disques durs, les entrées/sorties, les saisies claviers …

La différence entre les deux fichiers est que l’accès à /dev/random est bloqué si le système juge que l’entropie n’est pas suffisante tandis que /dev/urandom est toujours accessible. À l’exception du cas spécifique des clefs cryptographiques à longues durées de vie, /dev/urandom est suffisants pour tous les usages [URANDOM].

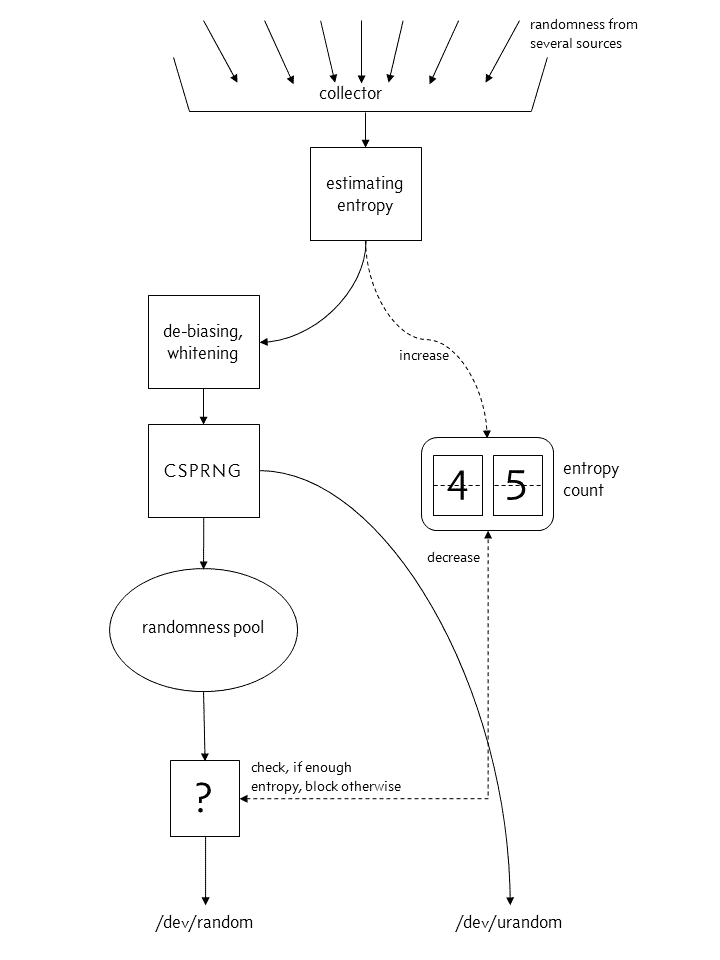
Il est également important de noter que tous les PRNG / CSPRNG sont périodiques, et finiront tôt ou tard à renvoyer la même suite de nombres qu’au début de leur initialisation (sauf en cas d’ajout d’entropie au cours de leur fonctionnement tel que le font /dev/random et /dev/urandom). Cette période dépend du type de générateur, et des paramètres internes du générateur.

Il existe une dernière catégorie de générateurs d’aléatoire : les TRNG, ou “True Random Number Generator”. Pour obtenir ce type de générateur, des sources physiques sont utilisées.

Par exemple, les désintégrations d’atomes instables peuvent être mesurées (à l’aide d’un simple compteur Geiger), et sont parfaitement imprédictibles car liées à la mécanique quantique.

Le bruit électromagnétique ambiant peut également être utilisé. Ce dernier est notamment perturbé par les orages et les appareils électriques environnants, dont l’activité est extrêmement chaotique.

On trouve aussi des détecteurs de muons, particules constamment générées dans la haute atmosphère lors de la collision de particules venant de l’espace, dont la présence à un instant spécifique et en un point spécifique d’un détecteur est parfaitement imprévisible (environ 10 000 muons sont reçus sur terre par mètre carré par minute).

Un des générateurs de nombres aléatoires de Cloudflare, LavaRand, est connu pour se baser sur la mécanique des fluides. L’idée est simple : récupérer le flux vidéo d’une caméra pointée sur des lampes à lave. Ce flux vidéo est utilisé comme source d’entropie, et est mixé avec d’autres sources.

C’est la répartition chaotique des pixels de l’image qui est “hashée” et utilisée comme source. Ainsi tout évènement impromptu, comme le passage d’une personne devant la caméra par exemple, permet de générer du bruit et d’enrichir le générateur.

Le dernier avantage de ce générateur est dû au fait qu’il incite les personnes le découvrant à se poser la question fondamentale « qu’est-ce que l’aléatoire ».

Un outil pour tester l’aléatoire : Random Test Tool

La motivation initiale de Random Test Tool (RTT) est de proposer un outil de test de générateur aléatoire qui soit facile d’installation et d’utilisation, mais aussi facilement modifiable.

Ainsi, RTT est développé en Python, ce qui lui permet d’être cross-platform mais aussi car c’est un langage fréquemment utilisé à la fois pour la création d’outils et pour des applications scientifiques. Plusieurs bibliothèques permettant de réaliser des opérations numériques/statistiques sont disponibles (Numpy, Scipy, pandas, statsmodel, …), et ont ainsi été utilisées pour l’implémentation de l’outil RTT.

Enfin RTT est disponible en open-source (licence MIT) à la fois sur Github, mais aussi via le gestionnaire de paquets PyPi (en cours de publication).

Présentation de RTT

Architecture et utilisation

L’outil RTT fonctionne en lançant des tests statistiques sur des fichiers contenant des nombres générés de manière aléatoire, puis il génère un rapport présentant les résultats de ces tests.

Plusieurs fichiers peuvent être fournis en entrée (options –input_files et –input_dir) et sont traités en parallèle grâce à l’option (–n_cores). Lors du lancement d’un run, on peut également sélectionner les tests à lancer (option –test) ainsi que le format du rapport de sortie (option –output).

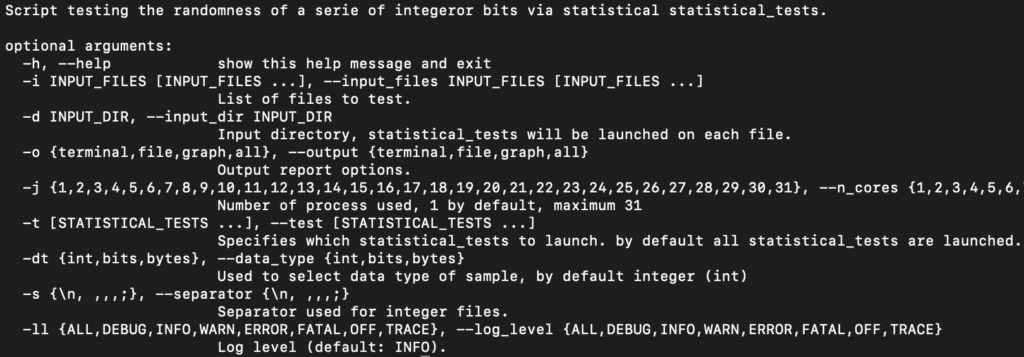
Pour le moment, RTT supporte trois types de formats d’entrées :

• Les « bitstrings », c’est-à-dire des fichiers sous la forme :

1010000111010010010011100110011

• Les « bytestrings » :

\x81\xce\xbdo\xcf

• Les suites d’entiers, pouvant être séparés par des saut de lignes, espaces, virgules et points-virgules :

1
12
43
24
1
3
8
13

Pour ce type de fichiers, seuls les intervalles contigus sont supportés.

Chaque fichier est ensuite traité par le processus suivant :

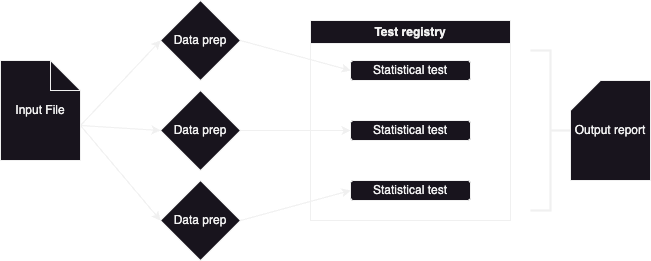
Les fichiers sont parsés, puis les données sont formatées pour chacun des tests sélectionnés pour l’exécution. Ensuite, les tests sont lancés successivement sur chacun des fichiers (en parallèle pour chaque fichier). Les résultats des tests sont enfin agrégés dans le rapport de sortie.

Pendant le traitement, une barre de progression informe de l’avancement actuel.

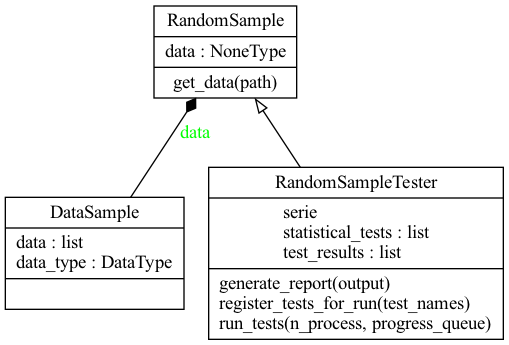
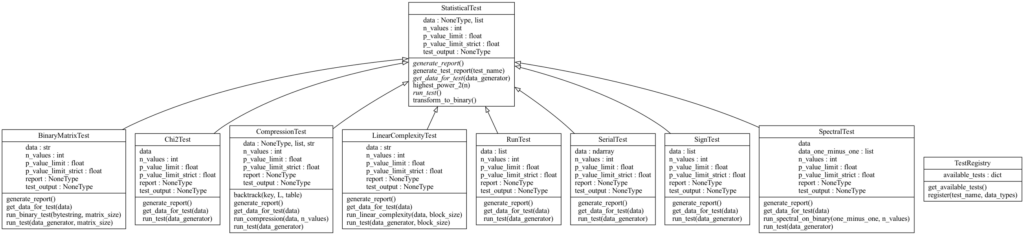
RTT est organisé autour de deux classes principales :

• RandomSampleTester responsable de l’exécution sur un fichier
• StatisticalTest qui est l’interface permettant l’implémentation d’un test statistique

Pour ajouter un nouveau test à l’outil, il suffit de le faire hériter de cette classe, d’implémenter les méthodes idoines et d’ajouter le nouveau test au registre (grâce à un décorateur Python). 

Le test est ensuite disponible pour être lancé via les options de lignes de commandes et intégré au rapport final.

Les formats de sortie disponibles sont les suivants :

• Rapport dans le terminal
• Rapport au format csv
• Production de graphiques

La version publiée de Random Test Tool est amenée à être améliorée. Notamment, les évolutions suivantes sont prévues :

• Ajout de nouveaux tests statistiques
• Amélioration des rapports de sortie afin de rendre le script automatisable
• Ajout de tests unitaires
• Ajout de la possibilité de paramétrer chacun des tests (constantes, p-values limites, …)

Tests statistiques

Les tests actuellement implémentés dans RTT sont les suivants :

Nom du test		Description du test
Chi-square	Vérifie l’adéquation de l’échantillon avec une distribution uniforme.
Sign	Vérifie l’égale répartition autour de la médiane.
Compression	Vérifie que la séquence ne peut pas être compressée sans perte d’information.
Run	Vérifie la répartition des séquences uniformes.
Serial de rang 2	Teste la distribution uniforme des paires de nombres.
Spectral	Vérifie la répartition des pics de la transformée de Fourier discrète de l’échantillon. Permets de détecter un pattern périodique.
Linear complexity	Teste la longueur des LFSR (Linear Feedback Shift Register) permettant de générer l’échantillon. Des LFSR trop petits signifient une séquence non aléatoire.
Binary rank	Vérifie la répartition des rangs des sous-matrices de taille fixe de l’échantillon. Permets de détecter une dépendance linéaire entre les blocs servant à générer les matrices.

Pour une description plus complète des tests, voir : [NIST-TEST-SUITE].

En sortie, chaque test donne la p-value obtenue sur l’échantillon ainsi que le statut :
OK/SUSPECT/KO.

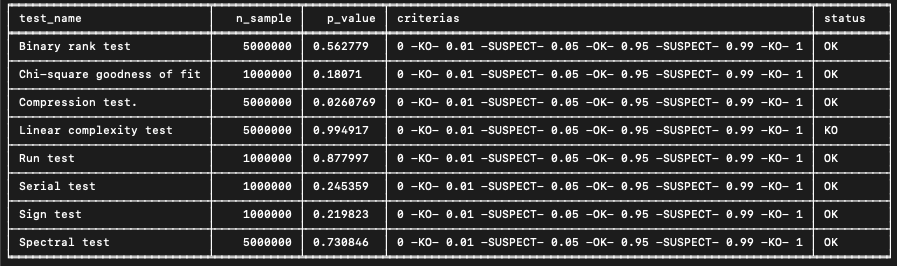
Par ailleurs, si la suite de tests est lancée sur plusieurs fichiers, on peut produire des graphes de type boîte à moustaches et nuages de points qui vont représenter pour chacun des tests la répartition des p-values pour les différents fichiers.

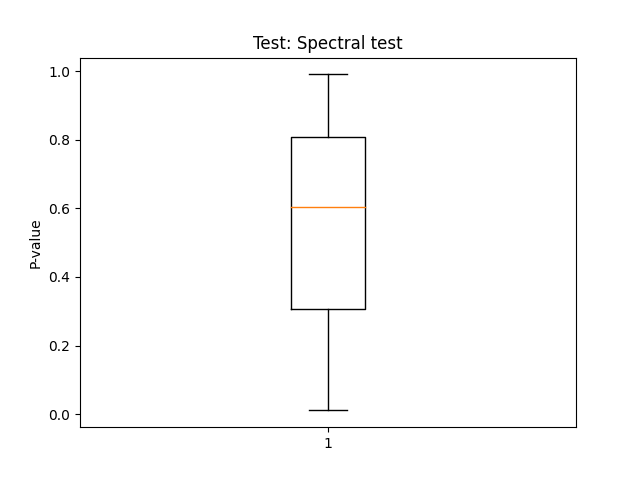
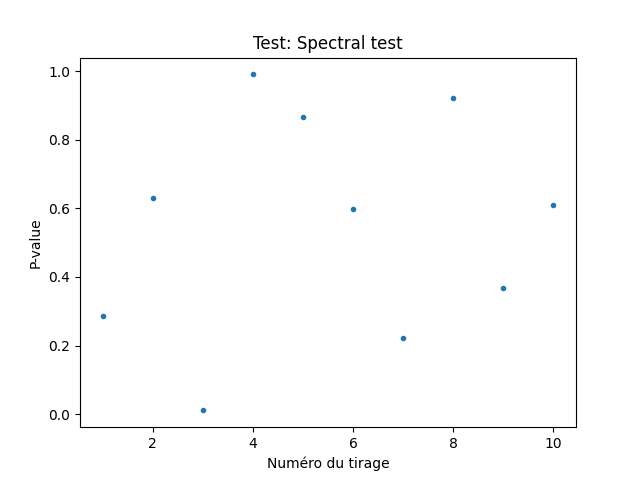
Pour un générateur aléatoire, la répartition des p-values devant être uniforme, ces graphes permettent de détecter visuellement une déviation par rapport à ce qui est attendu.

Test de RTT : résultats obtenus sur des générateurs pseudo-aléatoires

Procédure de test et résultats

Nous avons testé RTT sur des générateurs pseudo-aléatoires implémentés dans des langages de programmation courants. Les générateurs testés sont les suivants :

• Module random de Python
• Fonction $RANDOM de zsh
• Fonction $RANDOM de bash
• Classe Random de Java
• Fonction rand() de C
• Fonction Math.random() de Node.js
• Module rand de ruby
• Générateurs gonum/prng de Go

Pour tester un générateur, on commence par générer plusieurs échantillons de nombres ou de bits (entre 10 et 20). Chaque échantillon doit être suffisamment long pour être statistiquement significatif tout en évitant des temps de calcul trop importants. Nous recommandons des échantillons d’un million de nombres.

Chaque échantillon est ensuite testé par l’outil et les résultats des tests sont considérés indépendamment les uns des autres.

Sous l’hypothèse H0, où le générateur produit des nombres aléatoires, la distribution des p-values de chacun des tests doit être uniforme. Ainsi, pour déterminer le résultat pour un générateur donné, on regarde la déviation par rapport à cette attente. Selon l’ampleur de la déviation et le nombre de tests concernés, on qualifie chacun des générateurs en trois catégories :

• PASS : on valide l’hypothèse H0
• SUSPECT : à priori l’hypothèse H0 est rejetée, mais les résultats ne sont pas suffisamment significatifs pour le faire avec certitude
• FAIL : on rejette l’hypothèse H0

Prenons l’exemple du générateur $RANDOM de bash :

On lance la suite de test sur 10 échantillons de 1 million de nombres entiers. Les résultats obtenus pour chacun des tests sont les suivants :

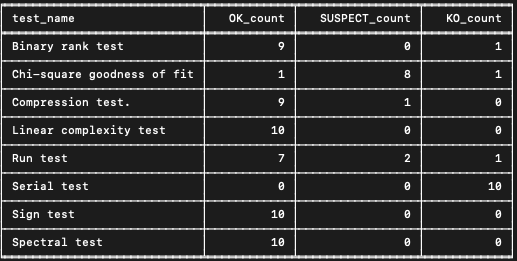
On remarque notamment 10 échecs pour le test Serial. La valeur-p limite pour ce test étant 0.01, un générateur aléatoire devrait avoir en moyenne 1 échec tous les 100 tests. Le nombre d’échecs sur ce test étant significativement supérieur à l’attendu, on en conclut que le générateur échoue le test Serial et qu’il n’est donc pas aléatoire.

Un nombre important de tests dans la catégorie « SUSPECT » indique un point d’attention :
il est nécessaire de refaire plus de tests. En effet seul un nombre significatif de « KO » permet de définitivement rejeter l’hypothèse H0.

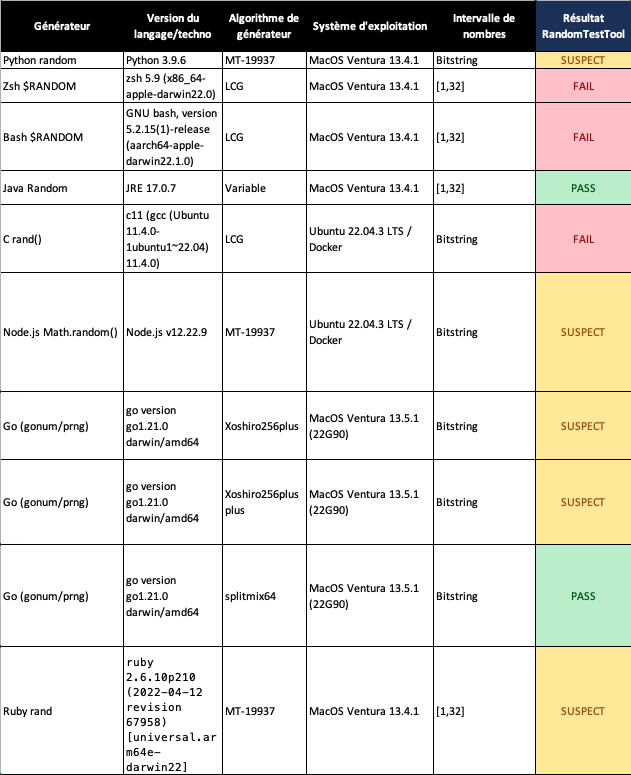
Dans le cas de résultats annotés SUSPECT, on réitère les tests sur un plus grand nombre d’échantillons (100 à 500) et on garde la conclusion donnée par cette seconde phase de tests.

Interprétation des résultats

Les générateurs testés précédemment sont connus pour ne pas être cryptographiquement sécurisés. [PRNG-LIST]

On s’attend donc à une proportion importante de tests qui échouent. Pourtant, les résultats obtenus sont aux antipodes de cet a priori.

En effet, les générateurs pseudo-aléatoires sont spécifiquement conçus pour avoir de bonnes propriétés statistiques et passent donc sans difficulté la plupart des tests. Pourtant cela ne veut pas dire que l’on peut utiliser ces générateurs à des fins cryptographiques !

Prenons l’exemple du module random de python qui a passé la plupart des tests statistiques de RTT. Le générateur pseudo-aléatoire de ce module se base sur l’algorithme Mersenne-Twister [PYTHON-RANDOM].  Les nombres générés par cet algorithme vont avoir de bonnes propriétés statistiques (bien que le test de Linear Complexity échoue pour ce cas en particulier). Pourtant, connaissant une suite de nombres générés par cet algorithme, il est possible de prédire l’intégralité des nombres suivants [PREDICT].

La qualité principale d’un générateur aléatoire cryptographique étant l’imprédictibilité de ses sorties, on ne peut donc pas utiliser le module random de Python pour ce type d’applications.

De manière générale, la connaissance de l’algorithme utilisé pour un PRNG permet au mieux de créer un algorithme permettant de prédire ses sorties ou du moins de créer un test spécifiquement dédié à sa détection.

Pour résumer, passer une suite de tests statistiques comme RTT doit être une condition nécessaire pour un CSPRNG, mais n’est pas une condition suffisante. Avoir de bonnes propriétés statistiques est indispensable pour un CSPRNG et désirable pour un PRNG, mais la preuve qu’un système de génération de nombre aléatoire est sécurisé doit passer non seulement par l’analyse statistique de la sortie, mais aussi par l’analyse de l’algorithme utilisé.

Bonnes pratiques

Afin d’éviter les vulnérabilités dues à l’utilisation d’un générateur de nombres aléatoires, un ensemble de points doit être vérifié. Ils sont décrits dans cette partie.

Bonnes pratiques d’implémentation

Les langages de programmation offrent souvent des méthodes permettant d’appeler des CSPRNG. En Python, la méthode os.urandom() permet par exemple de récupérer des nombres aléatoires depuis le périphérique /dev/urandom sur Linux, ou bien l’API Cryptographique CryptoAPI sur Windows.

Il convient d’utiliser ces méthodes plutôt que les PRNG par défaut (random dans le cas de Python) lorsque l’application nécessite un aléatoire de bonne qualité :

Génération de nombres aléatoires sécurisés
Langage de programmation	Méthode de génération cryptographique
Python	os.urandom()
C++	libsodium
Java	SecureRandom
C	libsodium
Node.js	node-sodium
C#	RandomNumberGenerator
PHP	openssl_random_pseudo_bytes

Si la méthode de génération de nombre aléatoire utilisée ne propose qu’une sortie de bits et qu’un nombre entier doit être sélectionné, alors une transformation doit être effectuée. Cependant, cette transformation n’est pas sans risque, et doit être effectuée en suivant certaines règles.

Prenons en exemple un générateur de bits aléatoires à partir duquel un nombre dans l’intervalle [1, 5] (5 valeurs) doit être tiré au hasard.

Exemple d’un algorithme de génération de nombres biaisé

Étant donné qu’à partir de 4 bits 8 valeurs différentes peuvent être obtenues, il peut être tentant d’utiliser l’algorithme suivant :

Nombre_entier_sur_4_bits = 4 bits générés aléatoirement  # intervalle [0, 7]

Nombre_aleatoire = (Nombre_entier_sur_4_bits modulo 5) + 1  # intervalle [1, 5]

Cependant, avec cet algorithme, la probabilité d’obtenir chaque nombre de l’intervalle [1, 5] n’est pas égale. En effet, chaque nombre de 1 à 3 aura 1 chance sur 4 d’être tiré, tandis que les nombres 4 et 5 auront chacun 1 chance sur 8 d’être tirés. Ce biais considérable peut aider un attaquant à gagner trop souvent au casino, même si un CSPRNG parfait est utilisé pour générer les bits aléatoires !

Exemple d’un algorithme de génération de nombres aléatoires sans biais

Deux solutions s’offrent ainsi à nous. La première, sans biais, est de recommencer le tirage (d’un nombre de bits permettant d’obtenir un intervalle suffisant) tant que la valeur obtenue n’est pas dans l’intervalle désiré :

FAIRE {
       Nombre_entier_sur_4_bits = 4 bits générés aléatoirement  # intervalle [0; 7]
} TANT QUE (Nombre_entier_sur_4_bits >= 5)  # Tant que le nombre tiré n'est pas dans l'intervalle [0; 4]

Nombre_aleatoire = Nombre_entier_sur_4_bits + 1  # intervalle [1; 5]

En effet, grâce à cette méthode, tous les nombres ont la même probabilité d’être tirés. L’inconvénient est qu’elle ne prend pas un temps constant. Certaines exécutions de ce script pourraient en effet demander 6, 7, ou encore plus de tours de boucle avant d’obtenir une valeur utilisable.

Exemple d’un algorithme de génération de nombres aléatoires avec un biais indétectable par les tests statistiques

La dernière solution que nous proposerons ici possède un biais, qui sera généralement acceptable et insignifiant, y compris dans des applications cryptographiques. Cette solution est proposée par le NIST. Elle consiste à tirer 64 bits de plus que le nombre de bits nécessaires pour obtenir tous les nombres de l’intervalle désiré (dans notre cas 4 bits, nous donnant un total de 68 bits). Elle peut être décrite ainsi :

Nombre_entier_sur_68_bits = 68 bits générés aléatoirement  # intervalle [0; 2^68 - 1]

Nombre_aleatoire = (Nombre_entier_sur_68_bits modulo 5) + 1  # intervalle [1; 5]

Cette solution fonctionne en un temps constant. En effet, aucune boucle n’est effectuée. Dans notre exemple, le biais obtenu est le suivant :

Le nombre 1 a 59 029 581 035 870 565 172 chances sur 2^68 d’être tiré.
Les nombres 2 à 5 ont chacun 59 029 581 035 870 565 171 chances sur 2^68 d’être tirés.

Note : Ce biais est dû au fait que 2^68 modulo 5 = 1. Par conséquent, 1 des 5 nombres de l’intervalle aura nécessairement une chance de plus d’être tiré.

Bien que le nombre 1 ait une probabilité plus grande d’être tiré, ce biais a été minimisé à un niveau considérablement faible, totalement indétectable.

Proposition de méthodologie “haut niveau” d’audit de générateur aléatoire

Afin d’auditer un générateur de nombre aléatoire, il est avant tout important de bien connaître les bonnes pratiques d’implémentation évoquées ci-avant.

Ensuite, les grandes étapes suivantes sont proposées afin de guider l’auditeur dans la réalisation de sa mission :

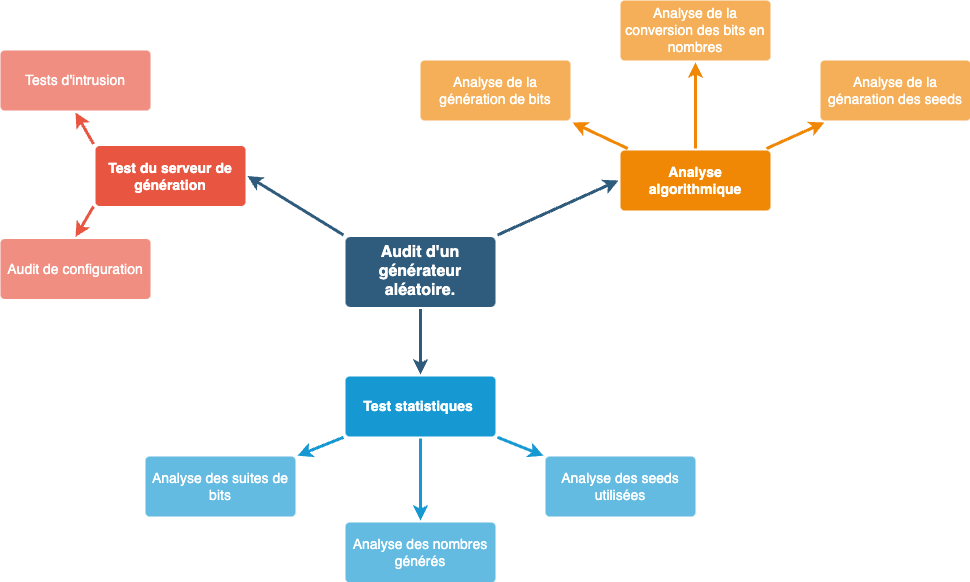
Un audit intégral de générateur aléatoire se décompose -a minima- en trois grandes étapes :

• Audit du serveur de génération : audit de la configuration du serveur et réalisation de tests d’intrusion afin d’évaluer la présence de failles de sécurité permettant à un attaquant de prendre le contrôle du serveur générant les nombres aléatoires.
• Tests statistiques :  réalisation de tests statistiques sur la sortie (ou les sorties) ainsi que sur les seeds utilisées pour valider la qualité statistique du générateur.
• Analyse algorithmique : audit de code des générateurs et processus de transformations des nombres pour confirmer que la connaissance du code source ne permet pas de déterminer les nombres générés.  Chaque algorithme doit être intégré spécifiquement pour chaque langage, en suivant les bonnes pratiques d’implémentation (cf. Section 3.1).

Synthèse des deux articles

Dans cette série de deux articles, nous avons pu constater que la génération de nombres aléatoires est utilisée dans de nombreux domaines du quotidien.

Certains de ces domaines sont critiques, comme la sécurisation des transactions bancaires par exemple, ce qui impose la validation des algorithmes utilisés pour ces applications.

La validation de la sortie des générateurs aléatoires par des tests statistiques est une part importante de ce processus de validation. Nous avons pu présenter un nouvel outil Python modulable et simple d’utilisation permettant de réaliser ces tests : Random Test Tool.

Néanmoins, ce processus de validation statistique n’est pas suffisant, comme nous avons pu le voir, les meilleurs algorithmes pseudo-aléatoires passent sans difficulté la plupart des tests statistiques. Ainsi l’analyse de l’algorithme utilisée est nécessaire pour réaliser un audit exhaustif d’un système de génération d’aléatoire.

Enfin, nous avons pu déterminer que de nombreuses solutions simples permettent de générer et d’utiliser des nombres aléatoires de haute qualité. Ce sont ces solutions qu’il faut privilégier lors de l’implémentation de programmes utilisant la génération de nombres aléatoires.

Antoine R & Nicolas G

Références

[ENTRO] https://scholar.harvard.edu/files/schwartz/files/6-entropy.pdf

[INFOR] https://fr.wikipedia.org/wiki/Th%C3%A9orie_de_l%27information

[ENTRO_FR] http://nomis80.org/cryptographie/node23.html

[ENTRO_MATH] https://kconrad.math.uconn.edu/blurbs/analysis/entropypost.pdf

[STATS] https://perso.univ-rennes1.fr/valerie.monbet/doc/cours/Cours_Tests_2009.pdf

[PVALUE] https://fr.wikipedia.org/wiki/Valeur_p

[CLOUDFLARE] https://blog.cloudflare.com/randomness-101-lavarand-in-production/

[URANDOM] https://www.2uo.de/myths-about-urandom/#from-linux-48-onward/

[NIST-TEST-SUITE] https://nvlpubs.nist.gov/nistpubs/legacy/sp/nistspecialpublication800-22r1a.pdf

[PRNG-LIST] https://en.wikipedia.org/wiki/List_of_random_number_generators

[PYTHON-RANDOM] https://docs.python.org/3/library/random.html

[PREDICT] https://github.com/kmyk/mersenne-twister-predictor